Class Daily Log
- MON : https://www.notion.so/Machine-Learning-iris-Classifier-Regression-PolynomialFeatures-Overfitting-Preprocessing-cleansi-1f074316415380779141c43d9f3c9219?pvs=4
- TUE : https://www.notion.so/Machine-Learning-classificaton-evaluation-1f174316415380f897b4c62665ba7dfd?pvs=4
- WED : https://www.notion.so/Machine-Learning-multiple-classificaton-evaluation-cross-validation-hyperparameter-tuning-1f27431641538090a487f8419e3e6492?pvs=4
- THU : https://www.notion.so/Machine-Learing-Regression-Gradient-Descent-Linear-Regression-Nonlinear-Regression-PipeLine-Reg-1f374316415380faa9d4d7011d445170?pvs=4
- FRI : https://www.notion.so/Machine-Learning-Recommendation-System-Content-Based-Collaborative-Filtering-Regression-Recommendat-1fc743164153800ca5dde4a9449ade49?pvs=4
✏️7주차 진행 내용 : Machine Learning ~ Deep Learning
📍이번주의 중요 내용
⭐SVM⭐
- Support Vector Machine (SVM)
- 써포트 벡터 머신
- 분류와 회귀 문제를 해결하기 위한 머신러닝 알고리즘
- 목표 : 데이터를 분류하거나 회귀선을 통해 예측하는 것
- 기본 개념
- 결정 경계(Decision Boundary) 또는 ⭐초평면(Hyperplane)을 찾아서 데이터를 두개 이상의 클래스 또는 회귀값을 기준으로 나누는 알고리즘
- 마진(Margin) ⇒ 초평면과 가장 가까운 데이터 포인트인 서포트 벡터 사이의 거리)을 최대화
- 커널 함수(Kernel Function) : 데이터가 선형적으로 분리되지 않는 경우, 커널 함수를 사용하여 저차원 데이터를 고차원으로 변환하여 초평면을 찾음
- 선형 커널(Linear Kernel)
- 비선형 커널(Non-linear Kernel)
- 다항 커널(Polynomial Kernel)
- rbf 커널
- 시그모이드 커널
- 가우시안 RBF 커널(Gaussian RBF Kernel)
- 핵심 요소
- 초평면 (Hyperplane) → 그림에서 중앙의 실선, 두 클래스를 최대한 분리하는 경계선
- 마진 (Margin) → 점선 두 개로 이루어진 띠, 초평면에서 가장 가까운 데이터 포인트(각 클래스의)까지의 거리
- 서포트 벡터 (Support Vector) → 마진 경계선(점선)에 딱 붙어 있는 점들

- SVM 종류
- Linear SVM
- Non-linear SVM
- ⭐SVM Classification(SVC) → 분류 문제에 사용 ⇒ 초평면을 찾으면 끝
- ⭐SVM Regression(SVR) → 회귀 문제에 사용 ⇒ 회귀계수를 가지고 띠를 만들고, 그 안에 잘 들어가도록 예측선(회귀선)을 만든다.
- 띠의 두께가 엡실론
⭐Ensemble Bagging, Boosting(XGBoost/LightGBM/CatBoost), Stacking, HyperOpt⭐
⭐Clustering(군집화) KMeans/DBScan⭐
⭐Deep Learning > Perceptron⭐
- 퍼셉트론
- 인공지능과 머신러닝의 기본 모델 중 하나, 인공 신경망의 가장 기본 단위
- 구성요소
- 입력 노드(Input Nodes)
- 가중치 (Weights, 기울기)
- 편향(Bias, 절편)
- 활성화 함수(Activation Function) → 1/0 만을 반환 (if z ≥ 0 1 else 0 ) ex) 계단 함수 Step function

- 한계
- 단층 구조로 구성되어 있기 때문에 선형 분리가 가능한 문제만 해결 가능
- XOR 문제와 같이 선형 분리가 불가능한 문제는 단일 퍼셉트론으로 해결할 수 X
- 단층 퍼셉트론한계
class Perceptron:
def __init__(self, W, b):
self.W = W
self.b = b
def activation_function(self, z):
"""계단 함수(Step Function)"""
# print(f'z = {z}')
return 1 if z > 0 else 0
def __call__(self, X):
"""현재 객체를 함수처럼 호츨할 수 있도록 하는 함수"""
return self.activation_function(np.dot(self.W, X) + self.b)
# and_gate 반환값 : 0 0 0 1
# or_gate 반환값 : 0 1 1 1
# nand_gate 반환값 : 1 1 1 0
# xor_gate 반환값 : 0 1 1 0
test_input = [(0, 0), (0, 1), (1, 0), (1, 1)]
# and_gate 반환값 : 0 0 0 1
# W, b 는 학습대상으로 원래는 찾아야 하는 값 (예제는 그냥 간단히 지정함)
and_gate = Perceptron(W=[0.5, 0.5], b=-0.7)
# __call__ 을 사용하였으므로 아래처럼 바로 호출 가능
for input in test_input:
print(input, ' -> ', and_gate(input))
"""
(0, 0) -> 0
(0, 1) -> 0
(1, 0) -> 0
(1, 1) -> 1
"""
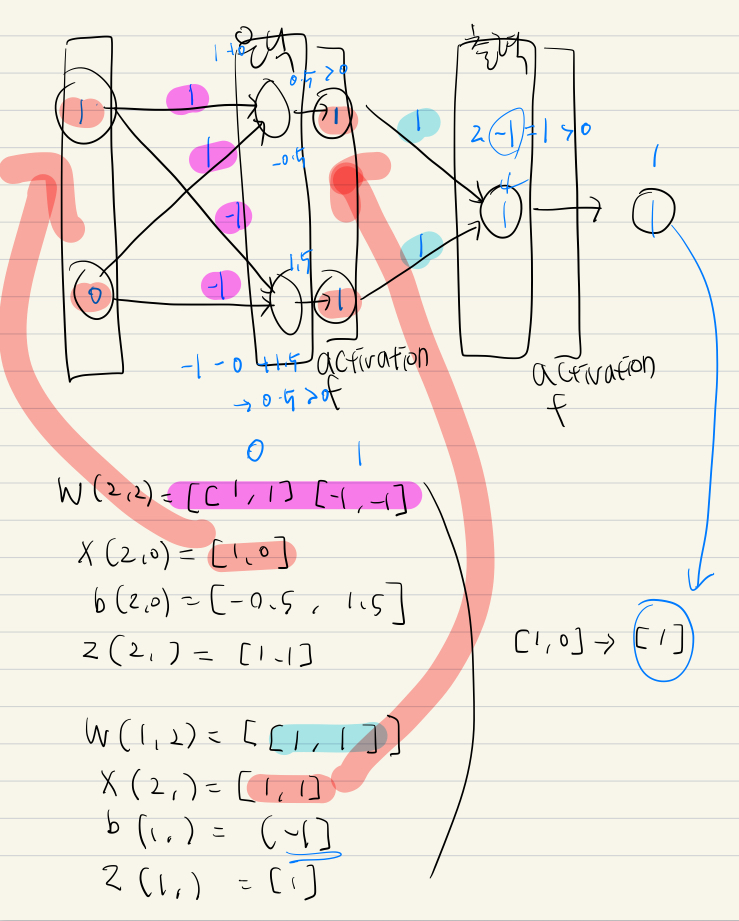
⭐Deep Learning > Multi-Layer Perceptron, MLP⭐
- 다층 퍼셉트론
- 단층 퍼셉트론의 한계를 극복하기 위해 여러 개의 퍼셉트론을 쌓아올린 형태
- 은닉층에 출력 (activative function 통해서 나온) 1/0 = 출력층의 입력
- 출력층의 출력 = 가중치 곱해서 더함(activative function 통해) 최종적인 아웃 풋 1/0

class MLP:
"""Multi-layer Perceptron"""
def __init__(self, W, b):
self.W = W
self.b = b
def activation_function(self, z):
return np.where(z > 0, 1, 0)
def __call__(self, X):
for W, b in zip(self.W, self.b):
print(f'\nW{W.shape}={W}')
print(f'X{X.shape}={X}')
print(f'b{b.shape}={b}')
X = np.dot(W, X) + b
X = self.activation_function(X)
print(f'z{X.shape}={X}')
return X
# XOR 해결을 위한 가중치/절편 준비
# 입력층(2) -> 은닉층(2) -> 출력층(1)
# 은닉측: 2개 노드(뉴런)
hidden_W = np.array([[1.0, 1.0],
[-1.0, -1.0]])
hidden_b = np.array([-0.5, 1.5])
# 출력층: 1개 노드(뉴런)
output_W = np.array([[1.0, 1.0]])
output_b = np.array([-1.0])
# 가중치/절편 처리
for i, (W, b) in enumerate(zip([hidden_W, output_W], [hidden_b, output_b])):
print(f'{i}:\n W={W}, b={b}')
"""
0:
W=[[ 1. 1.]
[-1. -1.]], b=[-0.5 1.5]
1:
W=[[1. 1.]], b=[-1.]
"""
# xor_gate
xor_gate = MLP(W=[hidden_W, output_W], b=[hidden_b, output_b])
inputs = [(0, 0), (0, 1), (1, 0), (1, 1)]
for X in inputs:
X = np.array(X)
y = xor_gate(X)
print('=' * 5, X.tolist(), '->', y, '=' * 5)
"""
W(2, 2)=[[ 1. 1.]
[-1. -1.]]
X(2,)=[0 0]
b(2,)=[-0.5 1.5]
z(2,)=[0 1]
W(1, 2)=[[1. 1.]]
X(2,)=[0 1]
b(1,)=[-1.]
z(1,)=[0]
===== [0, 0] -> [0] =====
W(2, 2)=[[ 1. 1.]
[-1. -1.]]
X(2,)=[0 1]
b(2,)=[-0.5 1.5]
z(2,)=[1 1]
W(1, 2)=[[1. 1.]]
X(2,)=[1 1]
b(1,)=[-1.]
z(1,)=[1]
===== [0, 1] -> [1] =====
W(2, 2)=[[ 1. 1.]
[-1. -1.]]
X(2,)=[1 0]
b(2,)=[-0.5 1.5]
z(2,)=[1 1]
W(1, 2)=[[1. 1.]]
X(2,)=[1 1]
b(1,)=[-1.]
z(1,)=[1]
===== [1, 0] -> [1] =====
W(2, 2)=[[ 1. 1.]
[-1. -1.]]
X(2,)=[1 1]
b(2,)=[-0.5 1.5]
z(2,)=[1 0]
W(1, 2)=[[1. 1.]]
X(2,)=[1 0]
b(1,)=[-1.]
z(1,)=[0]
===== [1, 1] -> [0] =====
"""
Keep
- 실습과제를 빼먹지 않은 것
- 복습을 그 날 못한 경우 다음날에라도 진행한 것
- 주 3일 이상 도시락을 싸간 것
Problem
- 점심 이후 오후 강의시간에 집중을 잘 못하는 것
- 평일 운동을 자주 하지 못한 것
Try
- 지하철 이용 시간에 독서나 Daily Log를 통한 복습을 진행할 것
- 복습을 미루지 말 것
- 평일에도 5/31 SQLD 시험 준비를 위한 공부 꼭 할 것
- 운동을 꾸준히 해서 체력을 늘릴 것
'교육 > SK네트웍스 Family AI 캠프' 카테고리의 다른 글
| [플레이데이터 SK네트웍스 Family AI캠프 14기] 9주차 회고 (1) | 2025.06.07 |
|---|---|
| [플레이데이터 SK네트웍스 Family AI캠프 14기] 8주차 회고 (1) | 2025.06.02 |
| [플레이데이터 SK네트웍스 Family AI캠프 14기] 6주차 회고 (1) | 2025.05.18 |
| [플레이데이터 SK네트웍스 Family AI캠프 14기] 5주차 회고 (1) | 2025.05.10 |
| [플레이데이터 SK네트웍스 Family AI캠프 14기] 4주차 회고 (0) | 2025.05.03 |



